 The animation illustrates an example of
such a mixed case,
in which a band of periodic waves is visible immediately behind
invasion, but develops into irregular oscillations further back.
The animation illustrates an example of
such a mixed case,
in which a band of periodic waves is visible immediately behind
invasion, but develops into irregular oscillations further back.
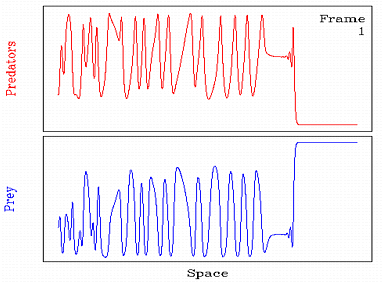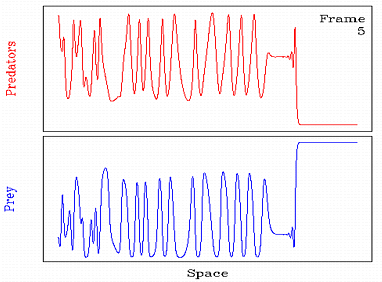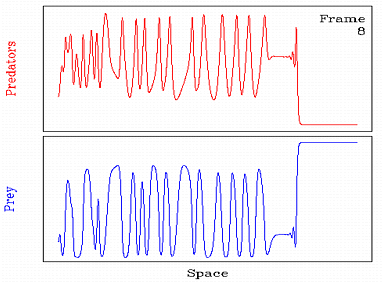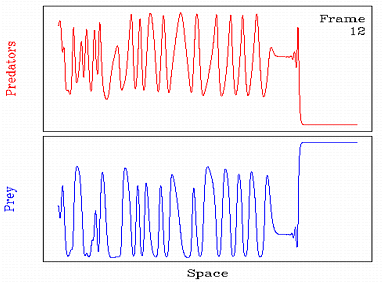
Invasion in cyclic populations
If a small group of predators is introduced into an otherwise
spatially uniform population of prey, the predators will tend to
invade the prey, leaving behind a mixture of predators and prey.
In collaboration with Mark Lewis, Barry Eagan and Andrew Fowler, I
have studied the behaviour behind such invasions for cyclic
populations. The results are somewhat suprising: the invasion leaves
behind spatiotemporal oscillations which fall into one of two
categories, either a periodic travelling wave or spatiotemporal
irregularity; mixed behaviour also occurs.
 The animation illustrates an example of
such a mixed case,
in which a band of periodic waves is visible immediately behind
invasion, but develops into irregular oscillations further back.
The animation illustrates an example of
such a mixed case,
in which a band of periodic waves is visible immediately behind
invasion, but develops into irregular oscillations further back.
Discrete Models
 These animations use a reaction-diffusion model, consisting of couple
partial differential equations for predators and prey. However we have
shown that the same phenomena occur in couple map lattice, cellular
automaton and integrodifferential equation models. The commonality
between these various models strongly suggests that the behaviour is
intrinsic to the underlying biology.
The figure shows a simulation of a couple map
lattice model for a parameter set giving a periodic wave behind
invasion. The colours represent predator density (white=zero, red=low,
blue=high).
These animations use a reaction-diffusion model, consisting of couple
partial differential equations for predators and prey. However we have
shown that the same phenomena occur in couple map lattice, cellular
automaton and integrodifferential equation models. The commonality
between these various models strongly suggests that the behaviour is
intrinsic to the underlying biology.
The figure shows a simulation of a couple map
lattice model for a parameter set giving a periodic wave behind
invasion. The colours represent predator density (white=zero, red=low,
blue=high).
Is it Chaos?
An important question is whether the irregular oscillations seen for
some parameter sets are genuinely chaotic. For the case of
reaction-diffusion models, I addressed this via a numerical
bifurcation study in which a fixed domain is consider, with domain
length taken as a bifurcation parameter. This reveals periodic
doubling and other well-known routes to chaos, as domain length is
increased.
Click to see a
 picture of period-doubling in an oscillatory system
picture of period-doubling in an oscillatory system
Which Periodic Wave?
Any oscillatory reaction-diffusion system has a family of periodic
travelling wave solutions. Therefore the process described above
raises a natural question: which member of this family is selected
behind invasion. This is an interesting mathematical question, but
is also important in applications, as the answer would enable
prediction of the speed and amplitude of the wavetrain,
and also its stability.
(The chaotic behaviour occurs when an unstable wavetrain is selected).
I have answered this question for systems that are close to a supercritical Hopf bifurcation in the reaction kinetics. Roughly, the calculation divides the solution up into three regions: the periodic wavetrain, the invading wave front, and the region in between these two. A solution is calculated in each region, and then matched up to give a final solution.
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)