Proceedings of the Conference on Nonlinear Coherent Structures in Physics and Biology,
Heriot-Watt University, Edinburgh, July 95

Ladder theorems and length scales in solutions of a generalized diffusion model

M. V. Bartuccelli ¹, S. A. Gourley

¹Department of Mathematical and Computing Sciences,
University of Surrey,
Guildford GU2 5XH, UK

Abstract

Length scales involved in dissipative partial differential equations are arguably one of the most important dynamical concepts for properly understanding the spatio-temporal patterns of dissipative flows. Here, a set of length scales for the solutions of the dissipative partial differential equation

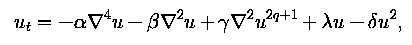
on periodic boundary conditions and in various spatial dimensions have been investigated. This model, in the case q=1, was first studied in the context of population dynamics by Cohen and Murray. Our length scales are based on ratios of norms, which involve a set of differential inequalities proved for the above equation. Lower bounds are derived for the time averages of these length scales.

SUBMITTED TO ``EUROPEAN JOURNAL OF APPLIED MATHEMATICS''

Conference paper.

ABSTRACTS
NextPreviousIndex
Last modified Mon Apr 8 16:24:53 GB-Eire 1996 (DBD)