Jonathan A. Sherratt, Department of Mathematics, Heriot-Watt University
Modelling the Movement of Interacting Cell Populations
Mathematical modelling of cell movement has traditionally focussed on
a single population of cells. However, many biological systems
actually involve two or more cell populations. In collaboration with
Kevin Painter, I have developed a simple partial differential equation
model for this situation.
A motivating example
Imagine a confluent sheet of cells, for example in a petri dish.
If a strip of cells
is removed from the sheet, the cells on either side of the
gap will migrate and divide in order to fill the gap.
 (This is a very simple example of wound healing).
The figure illustrates this process of gap creation following by healing.
As the cell populations on either side of the gap come together, they
will not intersperse significantly, because the cells stop moving
when they meet ("contact inhibition").
This is illustrated in the figure by pointing to it with the mouse.
The cell populations on either side of the gap appear in different
colours. This could be acheived experimentally by appropriate cell
staining.
Mathematically it is straightforward to formulate a partial
differential equation for the overall cell population. (The Fisher
equation is a good model, for example). But there is no standard model
in which the red and blue cell populations can be represented by
different variables.
The objective of our work was to develop such a model.
(This is a very simple example of wound healing).
The figure illustrates this process of gap creation following by healing.
As the cell populations on either side of the gap come together, they
will not intersperse significantly, because the cells stop moving
when they meet ("contact inhibition").
This is illustrated in the figure by pointing to it with the mouse.
The cell populations on either side of the gap appear in different
colours. This could be acheived experimentally by appropriate cell
staining.
Mathematically it is straightforward to formulate a partial
differential equation for the overall cell population. (The Fisher
equation is a good model, for example). But there is no standard model
in which the red and blue cell populations can be represented by
different variables.
The objective of our work was to develop such a model.
Equations based on space jump probabilities
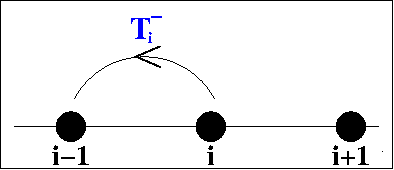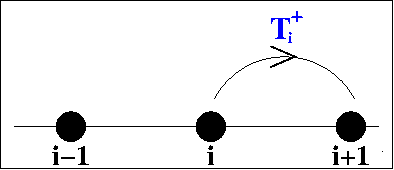 Kevin Painter and I dervied our model using "jump
probabilities". Assume that the cells move on a one-dimensional
lattice, with
T-i /
T+i
being the probability of moving from site i to site
i-1/i+1. Then it is straightforward to derive ordinary differential
equations for the cell density at each site and to then derive a
corresponding partial differential equation by taking an appropriate
limit. The equations vary according to the dependence of the transition
probabilites on the cell densities. The assumption that
T+i and
T-i
are independent of cell density gives separate linear diffusion terms
for the two populations, which would imply mixing of the red and blue
populations in the schematic figure above. But it is more realistic to
assume that the probability of the cell moving to the left/right is a
decreasing function of the cell density at the potential
destination. With suitable functional forms, this gives the model
equation and solutions show below.
Kevin Painter and I dervied our model using "jump
probabilities". Assume that the cells move on a one-dimensional
lattice, with
T-i /
T+i
being the probability of moving from site i to site
i-1/i+1. Then it is straightforward to derive ordinary differential
equations for the cell density at each site and to then derive a
corresponding partial differential equation by taking an appropriate
limit. The equations vary according to the dependence of the transition
probabilites on the cell densities. The assumption that
T+i and
T-i
are independent of cell density gives separate linear diffusion terms
for the two populations, which would imply mixing of the red and blue
populations in the schematic figure above. But it is more realistic to
assume that the probability of the cell moving to the left/right is a
decreasing function of the cell density at the potential
destination. With suitable functional forms, this gives the model
equation and solutions show below.
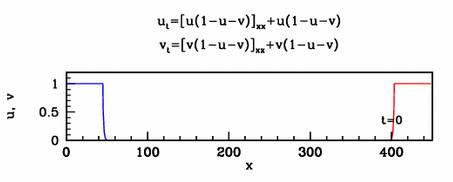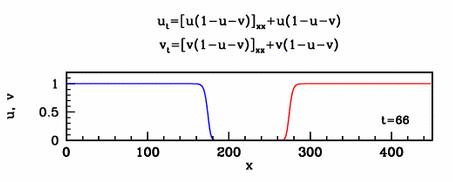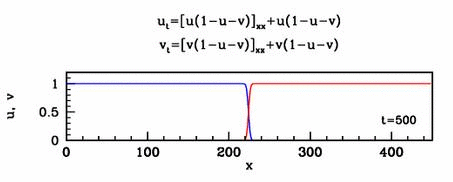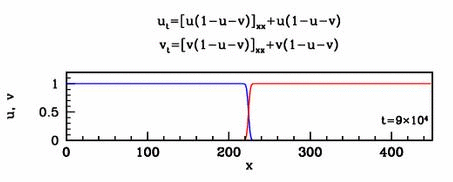
Applications
In collaboration with Mark Chaplain, I have
applied a simple form of the new model to early tumour growth. Many
other potential applications in developmental biology and physiology
remain to be explored.
Travelling waves
The nonlinear diffusion in the new model leads to unusual travelling
wave behaviour. For one special case of the new model, I have studied
this in detail. I showed that there are travelling wave solutions for
all speeds above a critical minimum value, a phenomenon familiar from
simple reaction-diffusion equations such as the Fisher
equation. However for this new model, I showed that the minimum speed
arises through a new and quite different mathematical mechanism.
The work described on this page is discussed in the following papers:
-
J.A. Sherratt:
Wave front propagation in a competition equation with a new motility
term modelling contact inhibition between cell populations.
Proc. R. Soc. Lond. A 456 2365-2386 (2000).
Click to see the
 Full paper (PDF)
Full paper (PDF)
-
J.A. Sherratt, M.A.J. Chaplain:
A new mathematical model for avascular tumour growth.
J. Math. Biol. 43, 291-312 (2001).
Click to see the
 Full paper (PDF)
Full paper (PDF)
-
K.J. Painter, J.A. Sherratt:
Modelling the movement of interacting cell populations.
J. Theor. Biol. 225, 327-339 (2003).
Click to see the
 Full paper (PDF)
Full paper (PDF)
Back to Jonathan Sherratt's Research Interests
Back to Jonathan Sherratt's Home Page
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 (This is a very simple example of wound healing).
The figure illustrates this process of gap creation following by healing.
As the cell populations on either side of the gap come together, they
will not intersperse significantly, because the cells stop moving
when they meet ("contact inhibition").
This is illustrated in the figure by pointing to it with the mouse.
The cell populations on either side of the gap appear in different
colours. This could be acheived experimentally by appropriate cell
staining.
Mathematically it is straightforward to formulate a partial
differential equation for the overall cell population. (The Fisher
equation is a good model, for example). But there is no standard model
in which the red and blue cell populations can be represented by
different variables.
The objective of our work was to develop such a model.
(This is a very simple example of wound healing).
The figure illustrates this process of gap creation following by healing.
As the cell populations on either side of the gap come together, they
will not intersperse significantly, because the cells stop moving
when they meet ("contact inhibition").
This is illustrated in the figure by pointing to it with the mouse.
The cell populations on either side of the gap appear in different
colours. This could be acheived experimentally by appropriate cell
staining.
Mathematically it is straightforward to formulate a partial
differential equation for the overall cell population. (The Fisher
equation is a good model, for example). But there is no standard model
in which the red and blue cell populations can be represented by
different variables.
The objective of our work was to develop such a model.
 Kevin Painter and I dervied our model using "jump
probabilities". Assume that the cells move on a one-dimensional
lattice, with
T-i /
T+i
being the probability of moving from site i to site
i-1/i+1. Then it is straightforward to derive ordinary differential
equations for the cell density at each site and to then derive a
corresponding partial differential equation by taking an appropriate
limit. The equations vary according to the dependence of the transition
probabilites on the cell densities. The assumption that
T+i and
T-i
are independent of cell density gives separate linear diffusion terms
for the two populations, which would imply mixing of the red and blue
populations in the schematic figure above. But it is more realistic to
assume that the probability of the cell moving to the left/right is a
decreasing function of the cell density at the potential
destination. With suitable functional forms, this gives the model
equation and solutions show below.
Kevin Painter and I dervied our model using "jump
probabilities". Assume that the cells move on a one-dimensional
lattice, with
T-i /
T+i
being the probability of moving from site i to site
i-1/i+1. Then it is straightforward to derive ordinary differential
equations for the cell density at each site and to then derive a
corresponding partial differential equation by taking an appropriate
limit. The equations vary according to the dependence of the transition
probabilites on the cell densities. The assumption that
T+i and
T-i
are independent of cell density gives separate linear diffusion terms
for the two populations, which would imply mixing of the red and blue
populations in the schematic figure above. But it is more realistic to
assume that the probability of the cell moving to the left/right is a
decreasing function of the cell density at the potential
destination. With suitable functional forms, this gives the model
equation and solutions show below.

 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)
 Full paper (PDF)
Full paper (PDF)