A Mathematical Model
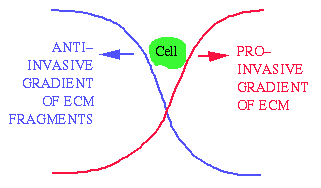 Abbey Perumpanani, John Norbury, Helen Byrne and I developed a
mathematical model to study the interaction between cell movement and
the breakdown of the extracellular matrix of surrounding tissue.
The model consists of coupled partial differential equations.
Roughly speaking, the invading cells create a gradient of
extracellular matrix around them, with more extracellular matrix ahead
of the cells (in the direction of invasion) and less behind.
The cells tend to move up gradients of extracellular matrix
("haptotaxis"), and thus invade the surrounding tissue.
Abbey Perumpanani, John Norbury, Helen Byrne and I developed a
mathematical model to study the interaction between cell movement and
the breakdown of the extracellular matrix of surrounding tissue.
The model consists of coupled partial differential equations.
Roughly speaking, the invading cells create a gradient of
extracellular matrix around them, with more extracellular matrix ahead
of the cells (in the direction of invasion) and less behind.
The cells tend to move up gradients of extracellular matrix
("haptotaxis"), and thus invade the surrounding tissue.
Anti-Invasive ECM Fragments
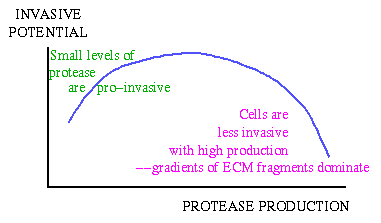 A complication is that the breakdown of extracellular matrix produces
fragments, which build up behind the invading cells. These have
traditionally been ignored, but in fact they also affect cell movement
- cells tend to move up gradients of these fragments as well as up
gradients of intact ECM. Our modelling shows that the anti-invasive
effect of these fragments is in fact very significant, and that
increasing enzyme production levels too much can cause cells to become
less invasive because the anti-invasive gradient of ECM fragments
dominates.
A complication is that the breakdown of extracellular matrix produces
fragments, which build up behind the invading cells. These have
traditionally been ignored, but in fact they also affect cell movement
- cells tend to move up gradients of these fragments as well as up
gradients of intact ECM. Our modelling shows that the anti-invasive
effect of these fragments is in fact very significant, and that
increasing enzyme production levels too much can cause cells to become
less invasive because the anti-invasive gradient of ECM fragments
dominates.
Experimental Confirmation
These predictions were partially confirmed by in vitro
experiments done by Abbey Perumpanani in collaboration with various
others including myself. We tested the ability of cells to crawl
through a micropore filter in the presence of artificially created,
opposing gradients of intact and fragmented extracellular matrix.
This showed that strong gradients of ECM fragments can override
gradients of intact ECM.
The Hole in the Wall
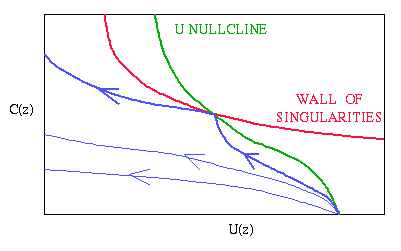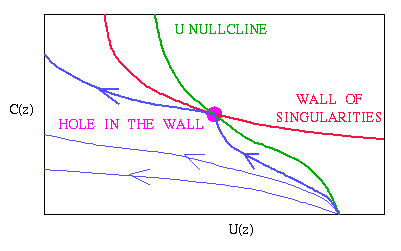 Mathematically, this model for invasion has some unusual behaviour,
which I studied in collaboration with Abbey Perumpanani, John Norbury
and Helen Byrne. The model
neglects any random component of cell movement, to focus on directed
motion, and thus the partial differential equations are hyperbolic.
Numerical simulations show that the solutions relevant to invasion are
travelling wave fronts. We assumed that the enzyme kinetics are at
quasi-steady state, in which case the travelling wave equations
consist of two ordinary differential equations containing a
"wall of singularities", i.e. a line in the phase
plane along which the equations are singular. One point on this line
is in fact non-singular (the intersection with a nullcline), and the
wave speed (i.e. invasion speed) generated from localised initial
conditions corresponds to a trajectory that just touches this "hole in
the wall of singularities".
In subsequent work, Ben Marchant, John Norbury and I considered the
corresponding travelling wave behaviour when the equation for enzyme
kinetics is retained. In particular, we show that a small amount of
protease diffusion is important for the formation of stable travelling
wave solutions.
Mathematically, this model for invasion has some unusual behaviour,
which I studied in collaboration with Abbey Perumpanani, John Norbury
and Helen Byrne. The model
neglects any random component of cell movement, to focus on directed
motion, and thus the partial differential equations are hyperbolic.
Numerical simulations show that the solutions relevant to invasion are
travelling wave fronts. We assumed that the enzyme kinetics are at
quasi-steady state, in which case the travelling wave equations
consist of two ordinary differential equations containing a
"wall of singularities", i.e. a line in the phase
plane along which the equations are singular. One point on this line
is in fact non-singular (the intersection with a nullcline), and the
wave speed (i.e. invasion speed) generated from localised initial
conditions corresponds to a trajectory that just touches this "hole in
the wall of singularities".
In subsequent work, Ben Marchant, John Norbury and I considered the
corresponding travelling wave behaviour when the equation for enzyme
kinetics is retained. In particular, we show that a small amount of
protease diffusion is important for the formation of stable travelling
wave solutions.
pH and Invasion
Steven Webb, Reginald Fish and I have also studied the effect of pH on
cancer invasion: this is important because of differences in pH
between tumours and surrounding normal tissue. Our modelling predicts
that these pH differences have a significant effect on the activity of
the cysteine class of proteolytic enzymes, but have little effect on
the activity of matrix metalloproteases. There is experimental
evidence that pH does alter the invasive potential of cancer cells,
and thus we conclude that cysteine proteases play a critical role in
cancer invasion. This prediction argues against the focus on matrix
metalloproteases in current experimental research.
The work described on this page is discussed in the following papers:
- A.J. Perumpanani, J.A. Sherratt, J. Norbury, H.M. Byrne: Biological inferences from a mathematical model for malignant invasion. Invasion and Metastasis 16: 209-221 (1996).
-
A.J. Perumpanani, D.L. Simmons, A.J.H. Gearing, K.M. Miller, G. Ward,
J. Norbury, M. Schneemann, J.A. Sherratt:
Does extracellular matrix mediated chemotaxis promote or impede cell
migration?
Proc. R. Soc. Lond. B 265: 2347-2352 (1998).
Click to see the
 Full paper (PDF)
Full paper (PDF)
-
A.J. Perumpanani, J.A. Sherratt, J. Norbury, H. Byrne:
A two parameter family of travelling waves with a singular barrier
arising from the modelling of matrix mediated malignant invasion.
Physica D 126: 145-159 (1999).
Click to see the
 Full paper (PDF)
Full paper (PDF)
-
S.D. Webb, J.A. Sherratt, R.G. Fish:
Alterations in proteolytic activity at low pH and its association with
invasion: a theoretical model.
Invasion and metastasis 17: 397-407 (1999).
Click to see the
 Full paper (PDF)
Full paper (PDF)
-
B.P. Marchant, J. Norbury, J.A. Sherratt:
Travelling wave solutions to a haptotaxis-dominated model of malignant
invasion.
Nonlinearity 14, 1653-1671 (2001).
Click to see the
 Full paper (PDF)
Full paper (PDF)
Back to Jonathan Sherratt's Research Interests
Back to Jonathan Sherratt's Home Page
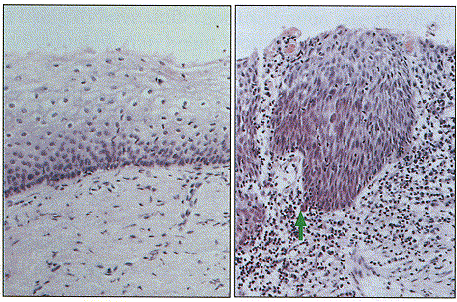 Solid tumours develop initially as a single mass of cells.
Cancer invasion is the process in which cells break away from this
primary tumour and crawl through surrounding tissue. This enables the
cells to move into a blood vessel and be transported through
the body, possibly establishing a secondary tumour at another site.
Cancer invasion involves a number of changes in cell behaviour, in
particular changes in motility and the production of enzymes that will
break down surrounding tissue.
Solid tumours develop initially as a single mass of cells.
Cancer invasion is the process in which cells break away from this
primary tumour and crawl through surrounding tissue. This enables the
cells to move into a blood vessel and be transported through
the body, possibly establishing a secondary tumour at another site.
Cancer invasion involves a number of changes in cell behaviour, in
particular changes in motility and the production of enzymes that will
break down surrounding tissue.