>

CALCULATION OF NORMAL FORM FOR PREDATOR PREY SYSTEM NEAR HO PF BIFURCATION AND APPLICATION TO PERIODIC WAVES GENERATED BY AN OBSTACLE

INITIAL SETUPS FOR MAPLE

> restart;

> assume(A>1);

> assume(B>0);

> interface(showassumed= 0);

DEFINE THE EQUATIONS

> f:=q->q/(1+q);

f := proc (q) options operator, arrow; q/(1+q) end ...

> fp :=P*(A*f(H*C)-1)/(B*A):

> fh:=H*(1-H)-P*f(H*C):

(these are the nondimensionalised population kinetics terms: as in equation (A.3) in the paper)

STEP 2 IN APPENDIX OF PAPER: STEADY STATES AND LINEAR STABILITY ANALYSIS

> Hs:=solve(A*f(H*C)=1,H);

Hs := 1/(C*(A-1))

> Ps:=A*Hs*(1-Hs);

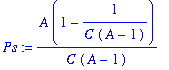
Ps := A*(1-1/(C*(A-1)))/(C*(A-1))

> tr:=1-2*Hs-Ps*C*subs(q=Hs*C,diff(f(q),q)):

> Ccrit:=solve(tr=0,C);

Ccrit := (A+1)/(A-1)

> det:=C*Ps*subs(q=Hs*C,diff(f(q),q))/(B*A):

> real_evalue:=tr/2:

> imag_evalue:=sqrt(det-tr*tr/4):

> Lambda0:=subs(C=Ccrit,diff(real_evalue,C)):

> Omega0:=subs(C=Ccrit,imag_evalue):

> Omega1:=subs(C=Ccrit,diff(imag_evalue,C)):

> simplify(Lambda0);

1/2*(A-1)/(A*(A+1))

> simplify(Omega0);

sqrt(A*(A-1)*(A+1)*B)/(A*(A+1)*B)

> simplify(Omega1);

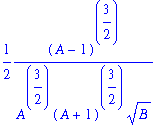
1/2*(A-1)^(3/2)/(A^(3/2)*(A+1)^(3/2)*sqrt(B))

NOW SET C=Ccrit

> C:=Ccrit:

> simplify(real_evalue); #CHECK ON VALUE -- SHOULD BE ZERO

0

> simplify(imag_evalue); #CHECK ON VALUE

sqrt(A*(A-1)*(A+1)*B)/(A*(A+1)*B)

STEP 3 IN APPENDIX OF PAPER: CONVERT LINEAR PART TO NORMAL FORM

> P:=Ps-phat*sqrt(A*(1-2*Hs)/B):

> H:=hhat+Hs:

> curlyF:=-fp/sqrt(A*(1-2*Hs)/B)+Omega0*hhat:

> curlyG:=fh-Omega0*phat:

NOW RUN SOME CHECKS ON curlyF AND curlyG -- there should be no linear terms

> simplify(subs(phat=0,hhat=0,curlyF));

0

> simplify(subs(phat=0,hhat=0,curlyG));

0

> simplify(subs(phat=0,hhat=0,diff(curlyF,phat)));

0

> simplify(subs(phat=0,hhat=0,diff(curlyF,hhat)));

0

> simplify(subs(phat=0,hhat=0,diff(curlyG,phat)));

0

> simplify(subs(phat=0,hhat=0,diff(curlyG,hhat)));

0

IF ALL SIX OF THE ABOVE GIVE ZERO, WE CAN CONTINUE.

STEP 4: CALCULATE LAMBDA1 AND OMEGA2

(using the formula given in the paper)

> Fpp:= subs(phat=0,hhat=0,diff(curlyF,phat$2)):

> Fph:= subs(phat=0,hhat=0,diff(curlyF,phat,hhat)):

> Fhh:= subs(phat=0,hhat=0,diff(curlyF,hhat$2)):

> Gpp:= subs(phat=0,hhat=0,diff(curlyG,phat$2)):

> Gph:= subs(phat=0,hhat=0,diff(curlyG,phat,hhat)):

> Ghh:= subs(phat=0,hhat=0,diff(curlyG,hhat$2)):

> Fppp:=subs(phat=0,hhat=0,diff(curlyF,phat$3)):

> Fpph:=subs(phat=0,hhat=0,diff(curlyF,phat$2,hhat)):

> Fphh:=subs(phat=0,hhat=0,diff(curlyF,phat,hhat$2)):

> Fhhh:=subs(phat=0,hhat=0,diff(curlyF,hhat$3)):

> Gppp:=subs(phat=0,hhat=0,diff(curlyG,phat$3)):

> Gpph:=subs(phat=0,hhat=0,diff(curlyG,phat$2,hhat)):

> Gphh:=subs(phat=0,hhat=0,diff(curlyG,phat,hhat$2)):

> Ghhh:=subs(phat=0,hhat=0,diff(curlyG,hhat$3)):

> Lambda1:=-(Fppp+Fphh+Gpph+Ghhh)/16+

> (Fpp*Gpp-Fhh*Ghh

> -Fph*(Fpp+Fhh)+Gph*(Gpp+Ghh))

> /(16*Omega0):

> Omega2:=(Gppp+Gphh-Fpph-Fhhh)/16+

> (Fpp*(Gph-Fhh)+Ghh*(Fph-Gpp)

> -3*Fhh*(Gph+Fhh)-3*Gpp*(Fph+Gpp)

> -2*(Fpp+Fhh-Gph)**2-2*(Gpp+Ghh-Fph)**2)

> /(48*Omega0):

> omega0:=(Omega0+mu*Omega1)/(mu*Lambda0):

> omega1:=-Omega2/Lambda1:

(Note: mu=C-C_crit)

END OF CALCULATION: NOW SIMPLIFY THE RESULTS

> simplify(omega0);

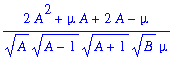
(2*A^2+mu*A+2*A-mu)/(sqrt(A)*sqrt(A-1)*sqrt(A+1)*sq...

> simplify(omega1);

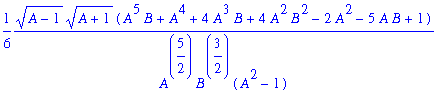
1/6*sqrt(A-1)*sqrt(A+1)*(A^5*B+A^4+4*A^3*B+4*A^2*B^...

CHECK VALUES FOR VOLE - WEASEL PARAMETERS

> subs(A=1.8,B=1.2,omega0);

12.60000000*(.3636964837+.2886480032e-1*mu)/mu

> subs(A=1.8,B=1.2,omega1);

1.238443900

NOW USE THE RESULTS TO TEST THE STABILITY OF PERIODIC TRAVELLING WAVES

GENERATED BY INVASION (WHEN MU=0)

> stability_test:=simplify(omega1**2);

> # Wavetrain is stable iff stability_test<1.233

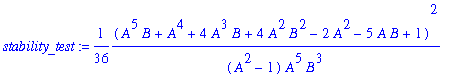
stability_test := 1/36*(A^5*B+A^4+4*A^3*B+4*A^2*B^2...

NOW VISUALISE THE STABLE/UNSTABLE PARAMETER REGIONS

(stable means stable periodic waves generated by bc;

unstable means spatiotemporal chaos generated by bc).

> with(plots): 

Warning, the name changecoords has been redefined

> istable:=0: iunstable:=0:

> Amin:=1.01: Amax:=6.9: Bmin:=1.01: Bmax:=10:

> npoints:=30: Astep:=(Amax-Amin)/(npoints-1): Bstep:=(Bmax-Bmin)/(npoints-1):

> for aa from Amin to Amax by Astep do

> for bb from Bmin to Bmax by Bstep do

> if eval(subs(A=aa,B=bb,stability_test))<1.233 then

> istable:=istable+1:

> Astable[istable]:=aa:

> Bstable[istable]:=bb

> else iunstable:=iunstable+1:

> Aunstable[iunstable]:=aa:

> Bunstable[iunstable]:=bb

> fi

> od

> od:

> stablepoints:={seq([Astable[i],Bstable[i]],i=1..istable)}:

> unstablepoints:={seq([Aunstable[i],Bunstable[i]],i=1..iunstable)}:

> stableplot:=pointplot(stablepoints,color=red,symbol=circle,thickness=2):

> unstableplot:=pointplot(unstablepoints,color=blue,symbol=box,thickness=2):

> neutrallystableplot:=implicitplot(stability_test=1.233,A=1.01..6.9,B=1.01..10,
color=green,thickness=3,numpoints=1000):

> unassign('ps');

> finalplot1:=display({stableplot,unstableplot,neutrallystableplot},

> labels=["A","B"],title="CIRCLE=stable, BOX=unstable"):

> plotsetup(default):

> finalplot1;

[Maple Plot]

THE END